Lambda calculus expressions can get really big, not only for actual encoded programs, but also for data encodings. This is because lambda calculus, due to its simplicity, doesn’t inherently support any kind of sharing or stored substitution bindings outside of abstractions.

For example, take the expression E=λx.(((M λy.N) M) λz.N). Its obvious encoding would always involve multiple copies of M, N. Not only that, but standard reduction strategies would needlessly evaluate the copied expressions multiple times.

One common way of solving this problem is to introduce let-bindings. This doesn’t really help me if I want to reduce and store pure lambda calculus expressions more efficiently, though.

There have been other solutions to the problem, notably by Accattoli et. al.. I, however, want to present an approach using hashes.

Goal

I want to generate a list of all expressions without any duplicates. The duplicates would then be referred to by some kind of index (e.g. memory address).

Let’s use the previous example expression E: Assuming M and N do not in turn contain existing terms, the list should, aside from the other constructs, contain only a single copy of N and M. Furthermore, the list should also only contain one copy of λy.<N> (with <N> being a reference to the actual N in the list).

Using this list would then make it easy to store the expression more efficiently (see BLoC), but more importantly, one could utilize the removed duplications to “parallelize” the reduction of such expressions.

Equivalence

Due to the complexity of the algorithms regarding $\alpha$-conversion and -equivalence, we convert the bound variables to de Bruijn indices.¹

Terms can then be represented using this abstract syntax tree (AST) definition:

data Term = Abs Term | App Term Term | Var Int

This enables us to derive an initial $\alpha$-equivalency algorithm:

equiv :: Term -> Term -> Bool
equiv (Abs x) (Abs y)         = (equiv x) && (equiv y)
equiv (App x1 x2) (App y1 y2) = (equiv x1 y1) && (equiv x2 y2)
equiv (Var x) (Var y)         = x == y
equiv _ _                     = False

Finding duplicate expressions would then come down to a quadratic brute-force search over all terms. I hope it’s obvious how this has a horrible time complexity – we need a different approach for evaluating equivalence.

Hashing

My main idea is to assign a hash to every sub-expression of an expression, such that comparing the hashes of two terms behaves the same as the previously described equiv function.

I assume a hash function $\mathcal{H}(d,s)$ with data $d$ and seed $s$. While the individual hashes should have a fixed size, we ignore hash-collisions for now by assuming that $\mathcal H$ is injective or perfect. A reasonable way of hashing lambda expressions would then be:

hash :: Term -> Hash
hash (Abs x)   = H 1 (hash x)
hash (App x y) = H (H 2 (hash x)) (hash y)
hash (Var x)   = H 3 x

There are obviously many different ways of doing this and the seed parameter isn’t actually needed at all. It makes it a bit easier to avoid collisions, though.

While we could now apply this function on every single sub-expression individually, we can also calculate the hashes in a bottom-up fashion.

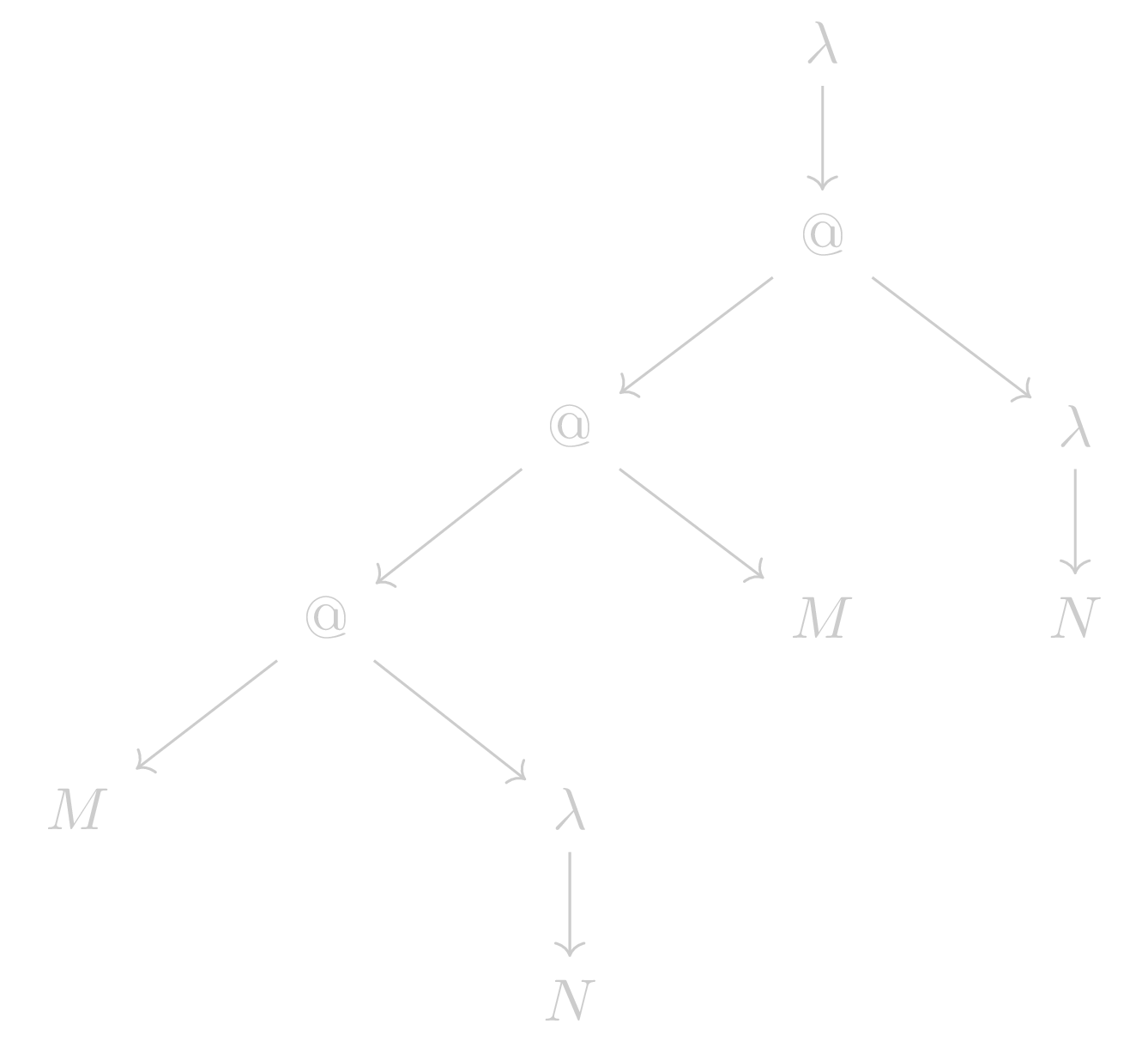
To give some intuition behind this part, let’s visualize the AST of E:

We now use the postorder tree traversal strategy (starting from the bottom left) to hash every sub-tree:

hash M -> hash N -> hash λN -> hash (M λN) -> hash M -> ...

This way, every parent just uses the previously calculated hashes of their child as input for their hash functions such that every term gets hashed exactly once.

Map

To get the desired result of a list of non-duplicate expressions, we can easily modify the tree traversal of the hashing procedure by adding the expression and its hash to a hashmap.

If we execute this procedure while constructing (e.g. while parsing) the expression in the first place, we potentially eliminate many redundant term allocations, as we can calculate the hash of an expression beforehand to check whether it exists in the hashmap already. The parent expression would then get the reference of the matching expression that was found in the hashmap. This reference could be a hash or a pointer. An implementation of this algorithm can be found in my calm project.

Collisions

The previously ignored problem of hash collisions is not easily avoidable. If a hash collision occurs, a parent might get a reference to the wrong expression. While it’s possible to detect a hash collision, by just comparing the sub-hashes (single level) of the existing expression in the hashmap, it’s not possible to bypass the problem completely (as far as I know).

During extensive testing using 64-bit hashes (xxHash), I never had a single hash collision – even with 500MB of bit-encoded BLC expressions. One way to further reduce the possibility would obviously be to use an even wider hash.

We could also store the bitwise BLC encoding of every term and use it in a mapping similar to a hashmap. This would keep the advantages of bottom-up building but would obviously have a massive time and memory complexity with big expressions.

Graph

Applying the described algorithm to E results in the following graph:

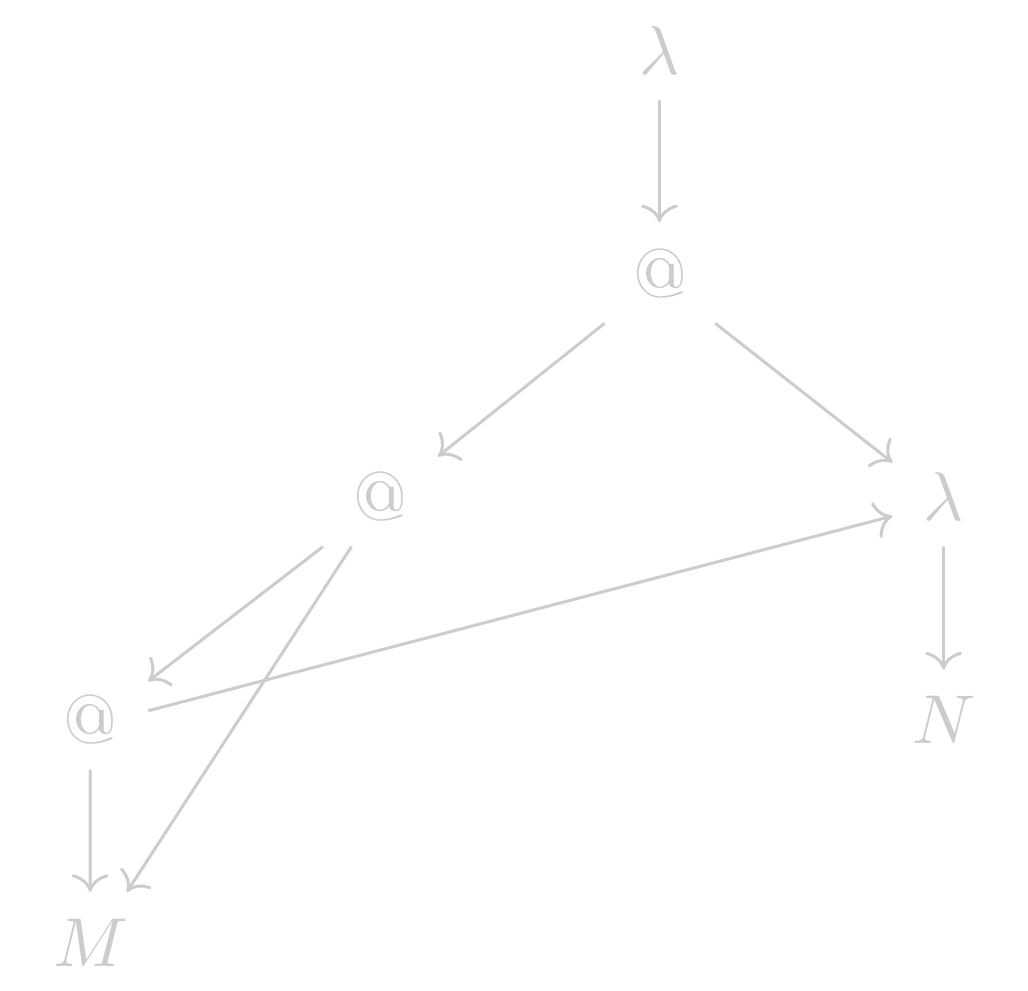
Such a graph is called a shared $\lambda$-graph and is – as a matter of fact – a directed acyclic graph (DAG), enabling us to apply many nifty tricks on it.

Conclusion

The derivation of shared $\lambda$-graphs from expressions in lambda calculus is essential for its efficient reduction and storage.

The presented algorithm achieves this with linear complexity while having the drawback of potential hash collisions.

You can find a full reference implementation including an algorithm for “sharing equality” here.

$$❦$$

Thanks for reading. Suggest improvements or fixes via email. Discuss on reddit. Support on Ko-fi.

动态网自由门 天安門 天安门 法輪功 李洪志 Free Tibet 六四天安門事件 The Tiananmen Square protests of 1989 天安門大屠殺 The Tiananmen Square Massacre 反右派鬥爭 The Anti-Rightist Struggle 大躍進政策 The Great Leap Forward 文化大革命 The Great Proletarian Cultural Revolution 人權 Human Rights 民運 Democratization 自由 Freedom 獨立 Independence 多黨制 Multi-party system 台灣 臺灣 Taiwan Formosa 中華民國 Republic of China 西藏 土伯特 唐古特 Tibet 達賴喇嘛 Dalai Lama 法輪功 Falun Dafa 新疆維吾爾自治區 The Xinjiang Uyghur Autonomous Region 諾貝爾和平獎 Nobel Peace Prize 劉暁波 Liu Xiaobo 民主 言論 思想 反共 反革命 抗議 運動 騷亂 暴亂 騷擾 擾亂 抗暴 平反 維權 示威游行 李洪志 法輪大法 大法弟子 強制斷種 強制堕胎 民族淨化 人體實驗 肅清 胡耀邦 趙紫陽 魏京生 王丹 還政於民 和平演變 激流中國 北京之春 大紀元時報 九評論共産黨 獨裁 專制 壓制 統一 監視 鎮壓 迫害 侵略 掠奪 破壞 拷問 屠殺 活摘器官 誘拐 買賣人口 遊進 走私 毒品 賣淫 春畫 賭博 六合彩 天安門 天安门 法輪功 李洪志 Winnie the Pooh 劉曉波动态网自由门